
|
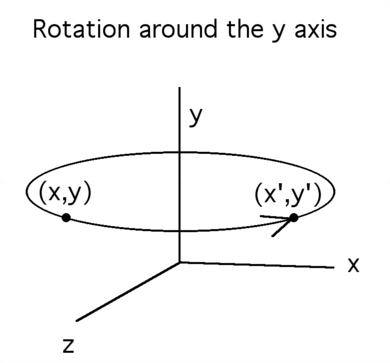
As the point revolves around
the y axis, it follows the path
of a circle, always at the same
height(y) and distance (the radius
of the circle) from the turning point
(the y axis).
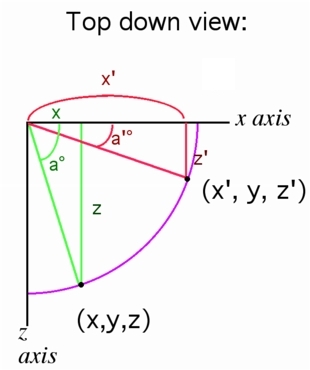
A green right triangle can be formed from the turning point, the original location (x,y,z) and the axes.
Since
Solving the equation for z,
Therefore, to get the new location (x', y, z')
we can see the red triangle can be formed,
and
By similar means the new x' will be
Since cos a° = adjacent/hypotenuse
and in the green triangle so that |
|
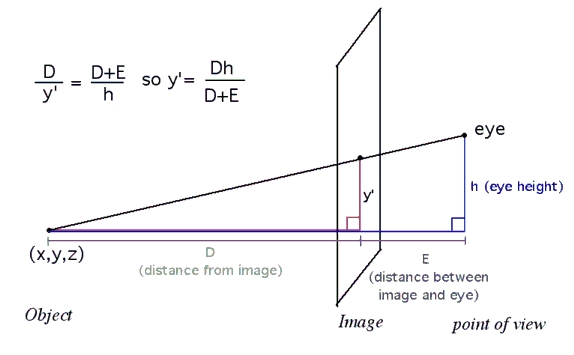
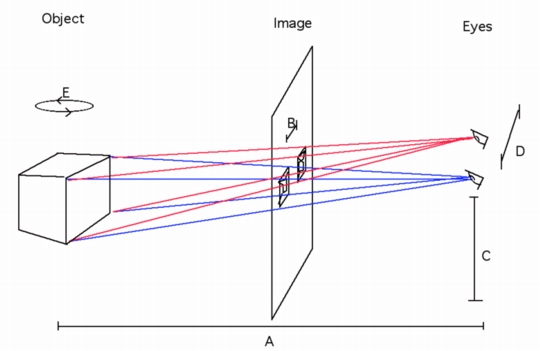
Secondly, you can see how the brain will even try to make two views from one in Single Image Random Dot Stereograms (SIRDS).
Finally, the computer can be fed new shapes, by describing the shape in terms of 3-D co-ordinates (x, y, z). See how you can make your own 3-D shapes here.