Instructions

Warning: Allow the Graphics and Java Applets to fully load before clicking anywhere

If you accidentally interupt the transmission before it is finished by clicking somewhere, you must press the "Refresh" button to start all over again from the beginning

The Questions YOU need to answer

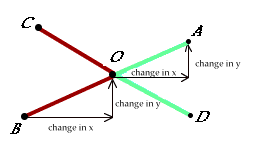
1. What is the measure of angle <AOC when A=(15,20)?

2. What is the measure of angle <AOD when A=(15,20)?

3. What is the name of the relationship between <AOC and <AOD?

4. What are the co-ordinates of point O (test your answer by moving point A there)?

5. What co-ordinates for point A make <AOC a right angle?

6. What co-ordinates for point A make <AOC a straight angle?

7. What co-ordinates for point A make <AOC a 60° angle?

8. Change the co-ordinates for point A but keep the identical 60° angle. What are the new coords?

9. Keeping A at (10, 20). Where can you place point B so that ray OD bisects <AOB?

10. Where can you place A and B so that <AOC is complementary to <BOD?

11. Move A to (10, 20). Where can you place point B so that <AOC is a vertical angle to <BOD?

12. Can you find a "formula" or express a "recipe" to generate the co-ords of the vertical angle?

    (Hint: Keep point B the same. Notice the horizontal and vertical change as it goes to O. Now you need to make the same changes to O to get to A. Check your work by making sure the angles match)

    

Click here to go to the Angle Page

Click here to go to The Elements

Click here if you have time

Send me e-mail (cct@ktb.net)