Heptadecagon
Carl Friedrich Gauss was born April 30, 1777 and when he was 19 years old, he proved that there was a way to construct a 17 sided regular polygon with only a compass and straight edge–something that escaped the ancient Greek mathematicians. This is how it is done:
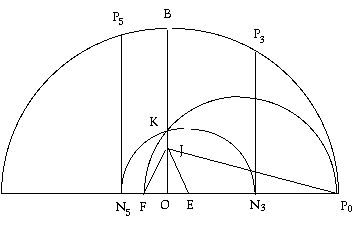
- Draw a circle around point O.
- Draw a diameter to form a Semicircle P0
- Find the perpendicular of OP0 and call it OB
- Find J a quarter the way up OB (bisect OB a couple of times)
- Join JP0 to form <
OJP
- Find E so that <
OJE is a quarter of <
OJP (Bisect is a couple of times)
- Find F so the <
EJF is 45° (bisect a perpendicular)
- Construct a semicircle from F to P0 (bisect FP0 to find the center of the semicircle)
- Find point K at the place this semicircle cuts across OB.
- Draw semicircle with center E and radius EK
- This cuts the extension of OP0 at N3 and N5
- Draw the perpendiculars through N3 and N3 to find P3 and P5
- P0, P3, P5 are the original, third and fifth points of the Heptagon.
Can you find a way to discover half the distance between P3 and P5 so you get the single length of one side? If you can then you can draw all 17 equal sides!

